Jouer avec les shaders

Après toutes ces explications un peu barbante (mais necessaires :p) sur les shaders, on va pouvoir commencer à jouer un peu. Vous allez pour l'instant travailler sur les deux shaders d'exemple qui ont l'avantage d'être simple.

Le triangle générique

Une fois n'est pas coutume, faites une copie du code du triangle en couleur. Nous allons faire en sorte qu'il puisse afficher un triangle en utilisant n'importe quel shaders passés en paramètre du programme. De cette manière vous n'aurez pas à dupliquer à nouveau du code pour les quelques exercices suivants.

Le paramètre argv de la fonction main (du code C++) est sensé contenir les arguments passés à l'executable. argv[0] contient le chemin vers l'executable. argv[i] pour i supérieur ou égal à 1 contient le i-ème argument passé au programme. Nous allons passer en premier argument le nom du vertex shader et en deuxieme argument le nom du fragment shader.

Modifiez le code C++ afin d'utiliser argv[1] et argv[2] pour charger les shaders. Compilez et essayez en passant à votre executable les deux shaders de l'exercice précédent:

TP2/TP2_exo2_triangleGenerique color2D.vs.glsl color2D.fs.glsl

Si vous avez bien codé, le triangle en couleur devrait à nouveau s'afficher.

Les types de GLSL

Pour réaliser les exercices suivants vous aurez besoin de manipuler des variables GLSL, en particulier des vecteurs et des matrices. Gardez la page suivante dans un onglet afin d'y piocher les informations dont vous aurez besoin: Data Type (GLSL)

Quelques conventions de code pour les shaders

Afin d'avoir un code GLSL plus clair, appliquez les conventions suivantes:

• Variables d'entrée du Vertex Shader: On les préfixe par un "a" (exemples: aVertexPosition, aVertexColor). Ce "a" signifie "attribute", pour signifier que la variable représente un attribut de sommet.
• Variables de sortie du Vertex Shader (et d'entrée du Fragment Shader): On les préfixe par un "v" (exemple: vFragColor). Ce "v" signifie "vertex", pour signifier que la variable sort du Vertex Shader.
• Variables de sortie du Fragment Shader: On les préfixe par un "f" (exemple fFragColor). Ce "f" signifie "fragment", pour signifier que la variable sort du Fragment Shader.

Le triangle des années 30

L'objectif de cet exercice est d'afficher le triangle en noir et blanc simplement en modifiant le fragment shader. Supposons que la couleur d'entrée est \((R,G,B)\), nous allons simplement fournir comme couleur de sortie le triplet \((M,M,M)\) avec \(M=\frac{R+G+B}{3}\).

Commencez par faire une recopie du fragment shader; renommez le grey2d.fs.glsl.

Modifiez le pour que le triangle soit affiché en noir et blanc comme indiqué dans l'énoncé (il suffit juste de changer une ligne). Testez le shader en utilisant votre executable du triangle générique (utilisez le même vertex shader qu'avant, ce dernier restant le même).

Transformation !

Il est possible de transformer votre triangle simplement en modifiant le vertex shader. Il suffit pour cela de modifier la ligne:

gl_Position = vec4(aVertexPosition, 0, 1);

En appliquant une opération sur aVertexPosition

Translatez le triangle selon le vecteur (0.5,0.5) (utilisez pour cela simplement une addition de vecteurs)

Doublez la taille du triangle (utilisez pour cela une multiplication par un scalaire)

Doublez la taille du triangle sur l'axe x et réduisez la de moitié sur l'axe y (utilisez une multiplication de vecteurs)

Une solution plus souvent utilisée pour transformer les vertex est d'utiliser des matrices. Afin de pouvoir appliquer les transformations 2D les plus utilisées (translation, rotation, scale) il est necessaire d'utiliser des matrices 3x3 ( la translation n'étant pas réprésentable par une matrice 2x2).

Soit \(P=(x,y)\) un point et \(M\) une matrice de transformation 3x3. Pour appliquer la transformation \(M\) a \(P\) on fait simplement une multiplication matricielle: \(P′=M×(x,y,1)\). On rajoute 1 à la fin du vecteur si on transforme un point. Dans le cas ou on transforme un vecteur on ajoute 0 (ce qui a pour effet de ne pas appliquer la partie translation, un vecteur n'ayant pas de position). En GLSL le vecteur que l'on récupère est de dimension 3; il faut le repasser en dimension 2 en gardant uniquement x et y. On pourra par exemple écrire:

vec2 transformed = (M * vec3(aVertexPosition, 1)).xy;
gl_Position = vec4(transformed, 0, 1);

On peut même se passer de la variable temporaire et directement ecrire:

gl_Position = vec4((M * vec3(aVertexPosition, 1)).xy, 0, 1);

Les matrices en GLSL sont dites column-major: on les stocke colonne par colonne. Par exemple si on ecrit :

mat3 M = mat3(vec3(1, 2, 3), vec3(4, 5, 6), vec(7, 8, 9));

Cela représente la matrice \(M = \begin{pmatrix} 1&4&7 \\ 2&5&8 \\ 3&6&9 \end{pmatrix}\)

De même l'accès aux valeurs d'une matrices par indice de tableau se fait en spécifiant la colonne en premier: la valeur 6 dans la matrice est accessible en écrivant en GLSL: M[1][2] (colonne d'indice 1, ligne d'indice 2). Il faut faire attention car c'est la convention inverse en mathématiques.

Voici la forme générale d'une matrice de translation: \( T_{tx,ty} = \begin{pmatrix} 1&0&tx \\ 0&1&ty \\ 0&0&1 \end{pmatrix} \)

Voici la forme générale d'une matrice de scale (non uniforme): \( S_{sx,sy} = \begin{pmatrix} sx&0&0 \\ 0&sy&0 \\ 0&0&1 \end{pmatrix} \)

Ecrivez deux fonctions dans le vertex shader: mat3 translate(float tx, float ty) et mat3 scale(float sx, float sy) qui renvoient les matrices correspondantes.

Refaites les transformations précédentes sur votre triangle (la translation et les scales) en utilisant cette fois des matrices.

Voici la forme générale d'une matrice de rotation d'angle α autour de l'origine: \( R_{\alpha} = \begin{pmatrix} cos(\alpha)&-sin(\alpha)&0 \\ sin(\alpha)&cos(\alpha)&0 \\ 0&0&1 \end{pmatrix} \)

Ecrivez la fonction mat3 rotate(float a) qui renvoit une matrice de rotation d'angle a (exprimé en degrés, faites la conversion avec la fonction radians de GLSL). GLSL vous permet d'utiliser les fonctions cos et sin (voir la doc pour une liste complète des fonctions GLSL).

Utilisez votre fonction pour appliquer une rotation de 45° à votre triangle. Le triangle doit apparaitre rotaté mais également déformé. Pouvez vous expliquer cette déformation ?

Combiner les transformations

L'avantage de représenter les transformations par des matrices est de pouvoir les combiner simplement en les multipliant.

L'ordre des transformations a une grande importance: la multiplication matricielle n'est pas commutative.

En pratique on combine toujours en multipliant à droite, c'est à dire en ajoutant les matrices à droite dans la liste de multiplication.

Il est important d'avoir une idée à peu près claire de ce qu'on va obtenir après avoir appliqué une suite de transformation. Lorsqu'on ajoute les transformations à droite, la façon la plus adaptée de penser est le modèle "local"

A chaque ajout de transformation la modification est faite sur le repère local de l'objet

Pour mieux comprendre observez l'image suivante:

Lorsqu'on ajoute la rotation de 45°, le carré tourne sur lui même, et non pas autour de l'origine. La transformation est donc appliquée sur son repère local et non sur le repère global.

De même quand on applique le scale, le carré se réduit sur lui même: c'est seulement le carré qui est scalé et non pas toute la scène.

En utilisant la multiplication matricielle, appliquez la suite de transformation du schéma sur votre triangle.

Modifiez l'ordre des transformations afin que la rotation s'applique autour de l'origine de la scène, tout en le gardant droit (à distance 0.5 de l'origine par exemple).

Pour les binômes, prenez une feuille. L'un des deux doit dessiner une position finale pour le triangle et l'autre doit coder la suite de transformations menant au résultat. Inversez ensuite les rôles. Si vous êtes seul, faites le pour vous même en essayant de ne pas imaginer les transformations en faisant le dessin.

Transformer le triangle en particule

Il est possible de dessiner une particule (ronde avec un halo) à partir du triangle simplement en travaillant sur les couleurs.

L'idée est assez simple: chaque fragment se trouve à une certaine distance du centre du triangle. Si on atténue sa couleur en fonction de cette distance, on peut générer une forme circulaire et le halo.

La formule d'atténuation a appliquer est la suivante: \(a=\alpha \times \exp(−\beta \times distance^2)\). Il suffira ensuite de multiplier la couleur finale par cette valeur. Vous devez faire varier les paramètre \(\alpha\) et \(\beta\) pour obtenir un résultat qui vous plait. Essayez de comprendre le rôle de chacun :)

Malheuresement pour vous, il y a un problème: pour calculer la distance du fragment au centre du triangle il vous faut la position du fragment (dans l'espace local du triangle, c'est à dire une position non transformée).

Cette position peut être obtenue en exploitant les variables d'entrée - sortie des shaders, un peu comme pour la couleur.

A vous de trouver comment obtenir la position du fragment :) Ensuite pour obtenir la distance vous pouvez utiliser la fonction... distance ! Modifiez le vertex et le fragment shader pour obtenir l'affichage d'une particule.

Voici le type de résultat à obtenir (j'ai repris un vieux screenshot, on peut faire mieux en faisant varier les paramètres:

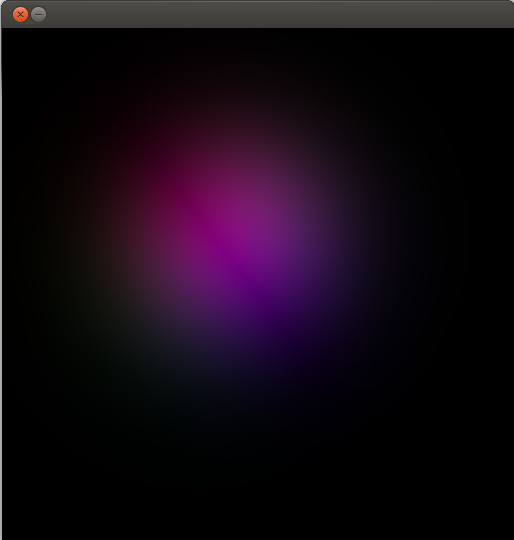
Combinez ensuite avec une transformation afin de voir si vous avez compris l'histoire d'espace local de coordonnées.

Textures procédurales

Le chargement et l'affichage de textures viendra plus tard. En attendant nous allons faire des textures procédurales pour notre triangle. Une texture procédurale est une texture calculée à la volée, avec des maths ! Vous pouvez voir le rendu sous forme de particule de l'exercice précédent comme une texture procédurale.

Il est possible de générer des patterns en combinant des fonctions simples comme fract, abs, smoothstep, mod, floor, ... Renseignez vous sur chacune de ces fonctions.

Voici quelques formules permettant de créer quelques patterns (\(P\) est la position du fragment dans l'espace local au triangle):

• length(fract(5.0 * P))
• length(abs(fract(5.0 * P) * 2.0 - 1.0))
• mod(floor(10.0 * P.x) + floor(10.0 * P.y), 2.0)
• smoothstep(0.3, 0.32, length(fract(5.0 * P) - 0.5))
• smoothstep(0.4, 0.5, max(abs(fract(8.0 * P.x - 0.5 * mod(floor(8.0 * P.y), 2.0)) - 0.5), abs(fract(8.0 * P.y) - 0.5)))

Chaque formule produit un coefficient que vous pouvez appliquer à la couleur du fragment (multiplication)

Essayez chacune des formules

Essayez ensuite de créer vos propre formules en combinant des appels aux fonctions de base de GLSL.

Et pour finir, une petite vidéo pour ceux qui sont interessés par le rendu procédural (3 min d'interview de Ignigo Quilez qui nous parle du rendu dans le film Brave de Pixar).