Dessiner une sphere

Le but de ce premier exercice est de dessiner une sphere. Commencez par repartir du template de base (SDLtemplate.cpp) afin d'avoir un code propre. Voici chacune des étapes à réaliser:

Créez une nouvelle variable de type Sphere à l'intialisation du programme (prenez comme rayon 1).

En utilisant la structure ShapeVertex et les méthode de l'objet sphere créé, construisez un VBO et un VAO contenant les sommets de la sphère.

Créez deux nouveau shaders 3D.vs.glsl et normals.fs.glsl. Le vertex shader doit prendre en entrée un sommet (3 attributs: position, normale, texCoords), trois matrices uniformes (4x4) uMVPMatrix, uMVMatrix et uNormalMatrix et calculer en sortie les position et normale en view coordinates, les coordonnées de texture sans les changer. Il doit également calculer la position projeté dans gl_Position. Essayez de coder ce shader from scratch (sans regarder l'exemple donné au cours du TP précédent). Le fragment shader doit prendre en entrée les variables de sortie du vertex shader et calculer en sortie la couleur du fragment. Comme couleur, utilisez la normale récupérée en entrée (normalisez la en utilisant la fonction normalize). Afficher la normale comme une couleur est une technique assez utilisée pour le debug.

Dans le code C++, chargez vos shaders afin d'obtenir un programme. Appelez la méthode use() afin de l'utiliser.

Toujours à l'initialisation, récupérez les location des variables uniformes (glGetUniformLocation) de vos shaders.

Ajoutez la ligne glEnable(GL_DEPTH_TEST); qui permet d'activer le test de profondeur du GPU. Sans cet appel de fonction, certains triangles non visible viendraient recouvrir des triangles situés devant.

Créez 3 variables de type glm::mat4: ProjMatrix, MVMatrix et NormalMatrix.

Calculez la matrice ProjMatrix en utilisant la fonction glm::perspective. Le premier paramètre est l'angle vertical de vue (mettez glm::radians(70.f)), le second est le ratio de la largeur de la fenêtre par sa hauteur (largeur / hauteur), les 2 derniers sont le near et le far qui définissent une range de vision sur l'axe de la profondeur: mettez 0.1f et 100.f.

Utilisez la fonction glm::translate pour calculer la matrice MVMatrix. La convention OpenGL est de regarder du coté négatif de l'axe Z dans l'espace View. Faites donc en sorte que la sphère soit dessinée en \((0,0,−5)\) via la translation qu'on lui applique.

Note: le fait de choisir near=0.1f et far=100.f pour la matrice de projection signifie que l'on ne verra que les objets situés entre -0.1f et -100.f sur l'axe Z (au risque de me répéter: car on voit du coté négatif des Z par défaut en OpenGL).

Calculez la matrice NormalMatrix en utilisant les fonction glm::inverse et glm::transpose sur la matrice MVMatrix.

Rappel: \(NormalMatrix=(MV^{−1})^T\), c'est à dire: glm::mat4 NormalMatrix = glm::transpose(glm::inverse(MVMatrix))

Dans la boucle de rendu à présent: remplacez la ligne glClear(GL_COLOR_BUFFER_BIT); par glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);. Cela permet de nettoyer le depth buffer à chaque tour de boucle.

A la suite, envoyez les matrices au GPU en utilisant la fonction glUniformMatrix4fv. Pour la matrice MVP, il faut envoyer ProjMatrix * MVMatrix. (N'oubliez pas d'utiliser la fonction glm::value_ptr pour récupérer le pointeur sur les données de chacune des matrices).

Enfin, bindez le VAO et utilisez glDrawArrays pour dessiner la sphère (on utilise ici glDrawArrays car le code de la sphere ne créé par de buffer d'index). Il faut dessiner des triangles et utiliser la méthode getVertexCount sur la sphère pour obtenir le nombre de sommets à dessiner. N'oubliez pas de débinder le VAO ensuite.

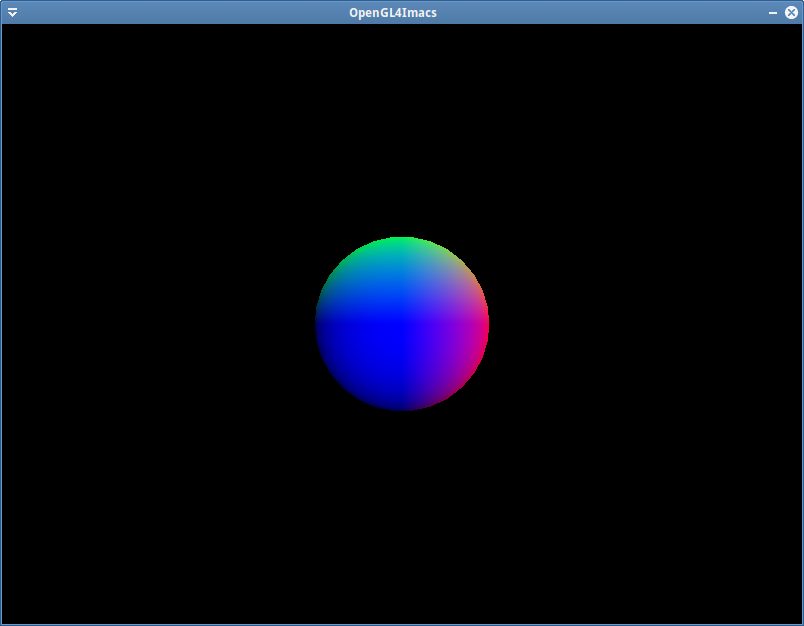
Testez, et bon courage pour le déboguage de votre premier (ou pas ?) programme 3D :D Voici le résultat attendu: