Freefly Camera

Ce type de caméra est utilisé dans les jeux à la première personne (les jeux ou on voit à travers les yeux du héros, comme les FPS). Elle permet de se déplacer dans toutes les directions et de tourner sur soit même (la caméra TrackBall ne permettant que de tourner autour du centre de la scène).

Sa ViewMatrix peut être calculé par un simple appel à la fonction glm::lookAt(eye, point, up). Le premier argument est simplement la position de la caméra exprimée dans le monde. Le deuxième argument est un point que la caméra regarde. Le dernier argument est l'axe vertical de la caméra.

Les arguments point et up doivent être calculés en passant par les coordonnées sphériques, illustrées ci dessous.

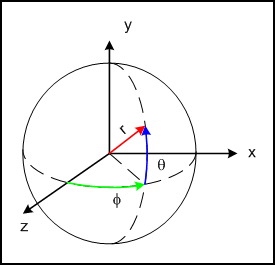
Les coordonnées sphériques \((\phi, \theta)\) sont les angles qui définissent le vecteur \(\vec{F}\) (qu'on appelera le "front vector") pointant en face de la caméra. On veut pouvoir controller ces angles en utilisant la souris. Notre objectif est de calculer les arguments point et up simplement à partir de la position P de la caméra (argument eye) et des angles \((\phi, \theta)\). Ces trois données seront stockées dans notre classe.

Le point de vue V (argument point) s'obtient simplement en additionnant le vecteur \(\vec{F}\) à la position: \(V=P+\vec{F})\) .

Il faut donc pouvoir calculer les coordonnées du vecteur \(\vec{F}\) en fonction de ses coordonnées sphériques \((\phi, \theta)\):

$$ \vec{F} = (\cos(\theta)\sin(\phi), \sin(\theta), \cos(\theta)\cos(\phi)) $$

(attention ici les angles sont exprimées en radians).

Il ne reste que le vecteur vertical \vec{U} (pour "up") à calculer. Pour cela nous allons utiliser le vecteur \(\vec{L}\) (pour "left") pointant à gauche car il nous resservira par la suite pour faire bouger la caméra latéralement. On a la relation suivante pour \(\vec{L}\) :

$$ \vec{L} =(\sin(\phi+\frac{\pi}{2}), 0, \cos(\phi+\frac{\pi}{2})) $$

Et pour \(\vec{U}\) :

$$ \vec{U} =\vec{F} \times \vec{L} $$

où \(\times\) est le produit vectoriel entre les deux vecteur (calculable avec la fonction glm::cross(F, L)).

C'est tout pour la théorie, passons à la pratique:

Créez la classe FreeflyCamera dans un nouveau fichier FreeflyCamera.hpp de la lib glimac. Elle doit contenir les variables membre glm::vec3 m_Position représentant la position de la caméra, float m_fPhi et float m_fTheta représentant les coordonnées sphériques du vecteur \(\vec{F}\) . Ajoutez également les variables glm::vec3 m_FrontVector, glm::vec3 m_LeftVector et glm::vec3 m_UpVector qui contiendront les vecteurs \(\vec{F}\) , \(\vec{L}\) et \(\vec{U}\) (ces variables sont redondantes puisqu'elles peuvent être calculés à partir des coordonnées sphériques, mais elles nous permettront de faire moins de calcul à chaque tour de boucle).

Écrivez la méthode privée computeDirectionVectors() qui calcule les vecteurs m_FrontVector, m_LeftVector et m_UpVector à partir des coordonnées sphériques m_fPhi et m_fTheta. Pour cela il suffit d'appliquer les formules données plus haut.

Écrivez le constructeur. La position de la caméra doit être initialisée à \((0,0,0)\). m_fPhi doit être initialisé à \(\pi\) (de cette manière le vecteur \(\vec{F}\) vaudra \((0,0,−1)\) et on regarde ainsi vers l'axe négatif des \(z\), convention en OpenGL). m_fTheta doit être initialisé à 0. Dans le corps du constructeur appelez votre méthode computeDirectionVectors afin que les vecteurs directionnels soit correctement initialisés également.

Écrivez les méthodes moveLeft(float t) et moveFront(float t). Ces méthodes doivent déplacer la position de la caméra respectivement le long du vecteur \vec{L} et \(\vec{F}\) . (déplacer un point P le long d'un vecteur V correspond à faire P += t*V).

Écrivez les méthodes rotateLeft(float degrees) et rotateUp(float degrees) modifiant les angles de rotations m_fPhi et m_fTheta (attention à convertir degrees en radians avant de faire l'addition avec les angles courants).

Écrivez la méthodes glm::mat4 getViewMatrix() const qui calcule et renvoi la matrice View associée à la caméra. Comme je l'ai dis plus haut, il suffit d'appeler glm::lookAt avec les bon arguments.

Reprenez le code précédent en utilisant cette fois la caméra FreeFly. Comme pour la caméra TrackBall, la caméra doit tourner lorsque la souris bouge alors que le bouton droit est pressé. Le déplacement doit être géré avec les touches Z, Q, S, D (comme dans un vrai FPS). La touche Z permet de bouger en avant, S en arrière, Q à gauche et D à droite.