Dessiner une lune

Afin de réaliser cet exercice, vous aurez besoin de récuperer le temps écoulé. Pour cela, j'ai ajouté la méthode getTime() à la classe SDLWindowManager. Téléchargez les fichiers SDLWindowManager.cpp et SDLWindowManager.hpp. Dans votre template de code (repertoire glimac), remplacez les anciennes versions par les nouvelles.

L'objectif à présent est de dessiner une lune tournant autour de notre sphère.

Dans notre cas une lune n'est rien de plus qu'une deuxième sphère, plus petite, placée relativement par rapport à la première.

Il va donc falloir dessiner deux sphère en changeant les transformations courantes avant chaque dessin. En particulier la matrice de transformation de la lune doit être en partie constituée de la transformation associée à la planète (puisque la lune tourne autour de la planète).

Pour dessiner une deuxieme sphere, il ne faut surtout pas créer un deuxieme couple VBO/VAO contenant les sommets d'une sphere plus petite. A la place on appelle juste deux fois la fonction glDrawArrays en modifiant les transformations avant chaque appel (on aura en particuler une transformation de type scale pour réduire la taille de la sphere).

Il est possible de combiner les transformations avec GLM en utilisant le premier paramètre de chaque fonction de transformation. Voici un exemple de code commenté:

glm::mat4 MVMatrix = glm::translate(glm::mat4(1), glm::vec3(0, 0, -5)); // Translation
MVMatrix = glm::rotate(MVMatrix, windowManager.getTime(), glm::vec3(0, 1, 0)); // Translation * Rotation
MVMatrix = glm::translate(MVMatrix, glm::vec3(-2, 0, 0)); // Translation * Rotation * Translation
MVMatrix = glm::scale(MVMatrix, glm::vec3(0.2, 0.2, 0.2)); // Translation * Rotation * Translation * Scale

La matrice passée en paramètre est multiplié à droite par la transformation demandée puis le résultat est renvoyé. Cela permet de recréer un concept de pile de transformation.

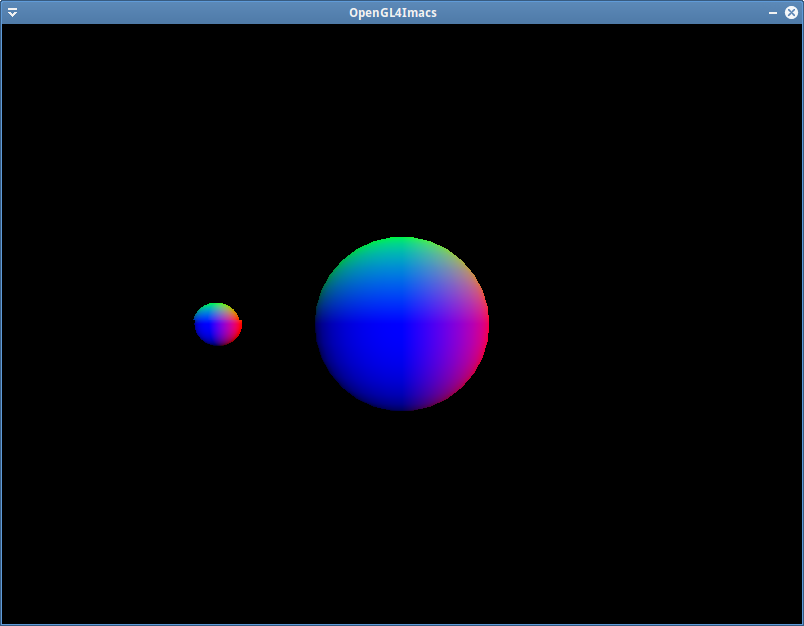
En utilisant des combinaisons de transformations, dessinez une lune. Dans un premier temps dessinez là immobile à gauche de la première sphère. Ensuite faites la tourner autour en utilisant comme angle de rotation le temps renvoyé par la méthode getTime() du windowManager.

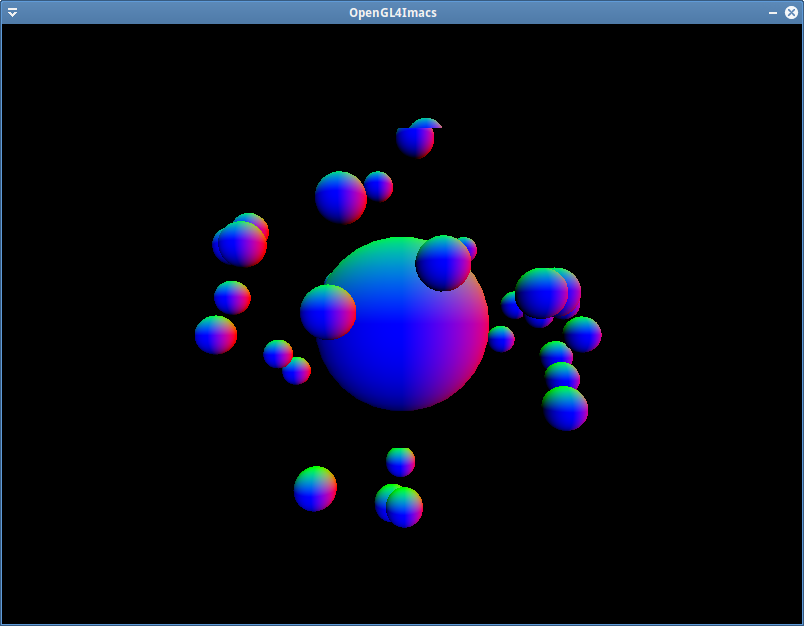
De la même manière, en utilisant une boucle, dessinez 32 lunes tournant autour de la planète, placées pseudo-aléatoirement. Pour cela il suffit de tirer l'axe de rotation aléatoirement. Avant la boucle rendu, utilisez la fonction glm::sphericalRand (documentation) pour tirer 32 axes de rotation que vous placerez dans un std::vector de glm::vec3. Utilisez ensuite ce vector dans la boucle de rendu pour dessiner toutes vos lunes. (il faut inclure le header glm/gtc/random.hpp pour utiliser glm::sphericalRand; rajoutez cet include dans le fichier glimac/include/glimac/glm.hpp). Testez le programme: il y a normalement un problème. Identifiez sa cause et corriger pour avec un résultat a peu près cohérent.